Mathematics of the Rubik's Cube
There are some serious questions about the mathematics of the Rubik's Cube. Fortunately most of these have been answered like what is the minimum amount of moves needed to solve it from any starting position or what is the number of possible permutations, and the list goes on.
After it had been invented nobody could solve it and they weren't even sure that a human being is able to unjumble it at all. It took a month to find the first solution of the Magic Cube despite almost every student was searching for it at the Budapest College of Applied Arts where the inventor, Rubik Erno was a professor back in 1974.
Number of permutations
Once I met somebody who has never played with the Rubik's Cube. He was sure about that he is able to solve it because it seemed so easy for him. "I just rotate the faces randomly until it is solved" - he said.
Well, it is not really so simple. There are so many possible states of a 3x3x3 Rubik's Cube you could never finish solving it just turning the faces randomly. Even a 2x2x2 Pocket Cube has 3.674.160 possible permutations. This strategy wouldn't work neither for a 2x2x2 cube.
The classic 3x3x3 has much more possible patterns: approximately 43 quintillion (exactly 43 quintillion, 252 quadrillion, 3 trillion, 274 billion, 489 million, 856 thousand). To illustrate this number, if we had as many 6 centimeter large Rubik's Cubes as there are permutations, we could cover the surface of the Earth 300 times.

For a 7x7x7 Cube this number is about 1.95 * 10160 roughly 19.5 duoquinquagintillion.
God's Number
God's Number shows the smallest number of moves needed to solve the 3x3x3 Rubik's Cube from any random starting position.
Since July of 2010 we know that this number is 20, so every position can be solved in twenty moves or less, considering one move a 90o or 180o twist of any face. This number was calculated thanks to Google who donated 36 CPU-years of idle computer time, solving every position of the Rubik's Cube in less than 21 moves. This means that we have found the solution of the "Superflip" scramble in 20 moves:
The first estimation of the God's Number was 52 moves in July 1981. Then this number was gradually decreasing. 42 in 1990, 29 in 2000, 22 in 2008, reaching the final number of 20.
We've written a separate article about the God's Number. Click here to read it!
Permutation Group
Mathematically the Rubik's Cube is a permutation group. It has 6 different colors and each color is repeated exactly 9 times, so the cube can be considered as an ordered list which has 54 elements with numbers between 1 and 6, each number meaning a color being repeated 9 times. We can rotate the 6 faces of the cube so we can define 6 basic operations or permutations which rearrange the ordered list in a certain way. Repeating and combining these permutations we can define new permutations, which rearrange the list in an other way. On the picture below you can see how a D rotation rearranges the elements of our list.
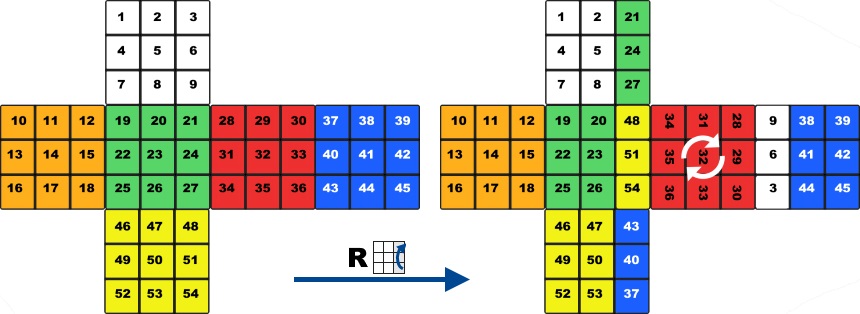
Now lets see why the Rubik's Cube is a permutation group. In math a permutation group is a group whose elements are permutations of ordered list, and whose group operation is the permutations which rearrange the set in a certain way. The group of all permutations of a set is the symmetric group.
Let's see the properties of this mathematic structure.
- Associative - the permutations in the row can be grouped together: ex. (RB')L = R(B'L)
- Neutral element - there is a permutation which doesn't rearrange the set: ex. RR'
- Inverse element - every permutation has an inverse permutation: ex. R - R'
- Commutative - Commutativity is not a necessary condition of the permutation group but notice that FB = BF but FR != RF
- Degree of permutations - this is a number which shows how many times has to execute a permutation to get back to the original position of the cube. Every permutation has a finite degree. ex: 4 x F = 1, 6 x (R'D'RD), 336 x (UUR'LLDDB'R'U'B'R'U'B'R'U) = 1
If you don't understand what the letters mean in the previous explication please read the notation.
This was just a very short introduction in the Mathematics of the Rubik's Cube, you can find much more interesting material about this topic. If you're interested I recommend you to read the paper of W. D. Joyner - Mathematics of the Rubik's Cube.