Bandaged Rubik's Cube Puzzles
 In search of more challenging puzzles, designers have gone many different ways. One of the first ideas was to extend the number of layers on the cube, producing such incredible puzzles as the 22x22x22 cube or the largest mass produced cube, the MoYu 13x13. However, the main method behind any numbered layer puzzle remained the same: Solving the centres intuitively, matching up edges by “slicing”, a process which temporarily distorts the solved centres, and then solving the cube using the outer layers, treating it as an oversized 3x3. People are continuing to delve deeper into methods such as mirror cubes (in which piece shape is used instead of colour to solve the cube), and cuboids which present the added challenge of shapeshifting and strange parities. However each of these methods have one thing in common – They all make the puzzle bigger, and aspects like shapeshifting add to this. Bandaging produces puzzles that look similar if not easier, and this deception fools many.
In search of more challenging puzzles, designers have gone many different ways. One of the first ideas was to extend the number of layers on the cube, producing such incredible puzzles as the 22x22x22 cube or the largest mass produced cube, the MoYu 13x13. However, the main method behind any numbered layer puzzle remained the same: Solving the centres intuitively, matching up edges by “slicing”, a process which temporarily distorts the solved centres, and then solving the cube using the outer layers, treating it as an oversized 3x3. People are continuing to delve deeper into methods such as mirror cubes (in which piece shape is used instead of colour to solve the cube), and cuboids which present the added challenge of shapeshifting and strange parities. However each of these methods have one thing in common – They all make the puzzle bigger, and aspects like shapeshifting add to this. Bandaging produces puzzles that look similar if not easier, and this deception fools many.
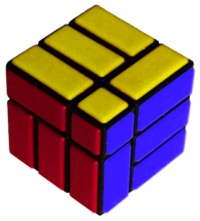
Uwe Meffert's Bandaged Cube design
The original Bandaged Cube, the Bicube by Uwe Meffert involved gluing some corner-edge pairs together to create 2x1x1 blocks. This presented an extra challenge to the original cube as, although the glued pieces could not be separated meaning the cube appears more solved once scrambled, many desired moves are impossible, and regular algorithms that you might have learnt from 3x3 or other puzzles can’t apply. On Jaap’s Puzzle Page, Jaap Scherpuis details the mathematical elements of the puzzle, proving that a maximum of 28 moves is required to solve the puzzle from any permutation.
Some types of cuboids can become bandaged when certain moves are performed, and entire blocks of pieces are left inseparable until the puzzle is un-bandaged. Shapeshifting puzzles in general have a problem with bandaging, an extra step to overcome to solve it. Some puzzles like the Ghost Cube are entirely bandaged, where moves can only be made by lining up several layers.
Different types of Bandagable Puzzles
A popular DIY bandagable puzzle is the Lego Rubik’s Cube. This involves removing the stickers (or tiles) from an original 3x3 Rubik’s Cube and replacing them with 2x2 Lego tiles in the same colour scheme. This can be used to create a normal 3x3 cube with Lego tiles, but for an extra challenge, you can attach 4x2 or 6x2 Lego pieces to the cube, effectively bandaging it. The best part of this cube is that if you can’t solve the bandaged puzzle, you can simply remove the extra pieces and solve it like a normal cube.

Another popular bandage puzzle is the Latch Cube. Unlike other bandaged cubes mentioned, this one doesn’t lock certain pieces together; each piece is separate and needs to be solved. However, each face has a circle on it, with an arrow in two opposite edge pieces. These indicate the direction the cube can be turned. When scrambled, there can be any number of arrows on any face. For faces with no arrows, the face can be turned either way. For faces with 1, 2, 3 or 4 arrows, if all arrows point in the same direction, the face can be turned in that direction. If one face has two arrows that point in different directions, the face can’t be turned.

Finally, there are the Constrained Cubes. These puzzles have modified centre pieces that prevent certain moves from being made. There are 4 different versions of this puzzle – Constrained Cube 90, 180, 270 and Ultimate. The larger the number, the easier the puzzle. For the Constrained Cube 90, only one quarter-turn can be made on each face, and the only two moves for any face is a quarter turn one way, and a quarter turn the opposite way. The 180 is similar, except you can perform a quarter or half turn on any face. The 270 is no extra challenge – if you can’t do a quarter turn in one direction, you can do 3 quarter moves the other way and end up in the same position.
The Ultimate is a combination of all of these puzzles. The white face is completely constrained so that it is unmovable, whereas the yellow face is completely free to move in any direction. The red and orange faces are constrained by 90 degrees, and the blue and green faces are constrained by 180 degrees.

