5x5x5 Rubik's Cube -How To Solve The Professor's Cube

The 5x5x5 Rubik's Cube also known as the Professor's Cube is the invention of Udo Krell. On this page I'm going to present this puzzle and will give you a clue about how to solve the 5 layered Rubik's Cube.

Manufacturers of the 5x5x5 include Rubik's, although their cube is loose and lock up easily. Another classic is the V-cube 5x5x5, which used to be the cube for competitions, however newer Chinese brand cubes are often faster. The Moyu Aochuang and Yuxin 5x5 are the two go to speed cubes on the market today, they don't lock up as often, are smoother and have some corner cutting capability.

Online 5x5x5 Rubik's Cube Simulator

2x2, 4x4 and 5x5 cube puzzles

There are not so many shape mods like the 2x2 and 3x3 but we have to mention the 5x5 mirror cube, the siamese versions and sticker mods.

The 5x5x5 Rubik's Cube puzzle has approximately 2,82 x 10⁷⁴ possible permutations. This number is close to the estimated number of atoms in the Universe.

The Solution Of The 5x5 Cube

The 5x5 is solved similarly to the 4x4x4 (or in fact, any NxNxN cube), which involves:

1. solving the centres
2. pairing up pieces to create the edges
3. finally solving like a 3x3 cube

Solving the centres

Centres are solved similarly to a 4x4x4, in which 'strips' of inner pieces are created and lined up in place. First create the centre strip around the centre piece (conventionally around the white centre), then create more and move them into place. Continue this until there are two adjacent centres to complete, in which case in like to treat as if I'm solving one of them, in which the other ends up solved.

To solve this puzzle you have to know the solution of the 4x4x4 Cube. We are using the same notation (letters in the algorithms) and the basic idea is also the same:

1. First we put together the centre 3x3 blocks,
2. then we pair the edge pieces,
3. then solve it like a regular 3x3x3 Rubik's Cube

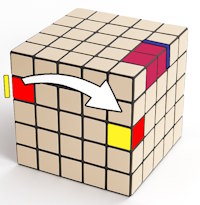
Pairing the edges:
Uw' R U R' Uw

This twisty puzzle might be even easier because it has fixed centre pieces, and there are no parity cases, but it takes more time to solve it because it has more pieces. Building the 3x3x3 is pretty intuitive, you have to use the same method you used in the case of the 4x4x4 cube.

Pairing the edges is a little different though. We'll have to place the two outer edge pieces next to the centre edge piece. To do this we're going to use the same Uw' R U R' Uw algorithm (and its symmetric) and we'll have to take care not to cut up the already solved pieces. You can see a blue line on the attached image where the pieces will be separated in the top layer. You can have paired pieces in the spots marked with pink without any problem because these will remain intact.

While pairing the edge pieces you might find yourself in a situation when you have to swap two edges like marked on the picture. You can't avoid using this longer algorithm when the two remaining edges are in this position and you don't have any unsolved edges to move in the top layer in the pink position. Do this algorithm, while holding the cube the way you see it on the picture:
Lw' U2 Lw' - U2 F2 Lw' F2 Rw U2 - Rw' U2 Lw2

When edge and the centre blocks are complete, just solve it like a 3x3x3 Rubik's Cube moving only the outer layers.

There are no parities on the 5x5x5 cube due to the cube having actual centre pieces. This means that for any NxNxN cube parities only occur when N is a even number.

Practice much with your 5x5 and you'll get into it!

Online 5x5 Simulator and Solver

Bjørn Kjos-Hanssen

I first used Instructables tutorial until I got stuck, then this page. A bit of trial and error later it was done! Thanks ⭐⭐⭐⭐

Paras Yadav

Awesome post man.I'd been stuck with edge exchanging problem for about half an hour. I applied the algorithm you've shown here and it solved instantly!!!

Darien Lim

This is poorly explained :(

Gia Huy Hua

You just a 𝓭𝓾𝓶𝓫 𝙣𝙤𝙣-🄲🅄🄱🄴🅁

Raven Skar

I garuntee you weren't always as good once either ya know....don't need to be rude. Dumb is asshats like you bashinhg on people calling them dumb, do you have a masters degree in all mathematics or anything that revolves around cubes like this with proof of a collage degree, probably not so perhaps don't judge people for different levels of intellect. I learned on my own how to do the 2x2, 3x3, 4x4 was my first time the other day and I nailed it in under 38 minutes, followed by the factor it only took me an hour to learn the windmill cube and the Skewb, some people even with cubing learn some faster than others, I can solve a 3x3 in under 40 seconds but I face some struggle trying to get the 5x5 down, how about instead of tearing people down you work on building others up and helping them understand what they don't know.

Kandan Mobley

I agree that it is only easy after you know how to do 3x3. Before that, especially the last steps, are not easy, even for someone who does have an engineering intellect.

Yes, it is easy now, and being just barely old enought to have held one of the first ones, I am amazed by how stupid I was at the age of six or so.

If they were so easy, there would be no point in doing them.

My favorites are the dodecohedrons and the mirror cubes. There is some issue I was/am running into with the 2x2 mirror cube, and I gave it to a buddy, and he eventually figured it out enough times that he thinks he can show me why I can't fit the last piece. And, to be noted here, it took him a rather long time to figure it out.

Maung Mic Maung

What the hell what is that u' R U R' u stuff?

Isaiah Lam

lol you need to know how to solve a 3 by 3 you 𝕚𝕕𝕚𝕠𝕥𝕤

Willem Keij

i do

Yolandi Dn

me too

Alz Birkill

Can you solve the intial 3x3 center by applying the algorythms as a normal 3x3 cube?

Will Bradley

no, you have to set them up in strips similar to the 4x4.

James Eugene Shallcross

to the ones complaining about how its not in depth, he literally says that you have to know how to do 3x3 and 4x4, if you are doing 5x5 and can't do the first 2, you need to re-evaluate your lifestyle

Keith Hill

THIS PROGRAM SOLVES NOTHING

Robert Baker

The statement that there are "no parity cases" is incorrect; I've just attempted to use the second algorithm (having already solved the centres without any help), and have arrived at the situation where 11 of the edges are correct and the 12th has its centre flipped -- definitely a parity problem.

Anh Nguyen

What you are saying is not parity; you simply built the wrong centers. You need to match the exact color scheme of a normal cube first color schemes . Even if you mess up only two faces, the cube would be unsolvable, it seems like parity but it's not. Odd layered cubes don't have parity, since the centers are fixed.

Edit: After re-reading your comment, I finally understood what you were saying. What you have there is still not parity, it's just an unfortunate edges-pairing case (People still (humorously) call it parity because it's also a pain to fix like even-layered cubes' parity). Refer to this to fix the last 2 edges:

Will Bradley

Anh Nguyen I asked my genius friend about this problem. This is his response: " Imagine a 3x3 cube is a special case of a 5x5 cube. The degrees of freedom are reduced. In the 4x4 case it is a 5 cube but the middle rows are invisible. In the case of edge parity, the middle row is properly aligned but the inner two around it are flipped. This occurs in the 4 cube case but the effects are only apparent when solving the last face."

Will Bradley

so technically it is parity because the 5x5 with an invisible middle layer is a 4x4 thus causing the odd swap.

Katja Shutes

i am out this is so confusing

Anh Nguyen

Ok, for everyone who is complaining, why would you want to solve a 5x5 when you don't know how to solve a 3x3 or even a 4x4? Would you want to learn calculus without knowing any algebra or arithmetic? This page only adds more useful steps needed to solve a 5x5 with the known steps from solving a 3x3 and 4x4. It is literally stated as the first sentence: "To solve this puzzle you have to know the solution of the 4x4x4 Cube" (which also includes knowing a 3x3 solution). So stop whining and actually appreciate the fact that there is a 5x5 guide up for grabs.

Johair Raniai Jamail

True dat

Olle Borg

This is crap, really. It covers two situations where the faces of the pieces are not given! - Well, the first is trivial, but the second is definitely not. Most importantly (as it is not part of the 4x4x4 solution), it does not cover the situation (during "pairing the edges") when only one pair is left and the center edge is flipped. Please fix!

Ethan Lee

Lw' U2 Lw' U2 F2 Lw' F2 Rw U2 Rw' U2 Lw' Lw'

Will Bradley

this is the only thing they were missing, thank you!

Buck Frank

You won't need this EVER if you group the edges first with the shorter Lw' U2 Lw' - U2 F2 Lw' F2 Rw U2 -Rwr' U2 Lw2. You shouldn't start solving the cube as a 3x3 before grouping the edges and centers.

Maung Mic Maung

This thread is a beautiful example of people being stubborn dumbasses and refusing to listen, while simultaneously asking for help with said thing that they wont listen about

Joakim Jacobsson

they say it has no parity. but it does!
Rw U2 x Rw U2 Rw U2 3Rw' U2 Lw U2 Rw' U2 Rw U2 Rw' U2 Rw'

Gia Huy Hua

You will never need this if you group the edges first. You shouldn't start solving it as a 3x3 before grouping the edges and centers.

Jim Lam

100x100x100 rubik's cube, please

Elgin Rahardja

I only know 3x3 but i solved until last 2 edge without tutorial/algs

Brad Lichtenstein

By following the 4x4 instructions, everything went fine until putting together the last pair of edges. They ended up with some sort of parity, false or not: all the edges were aligned, but one; and that one had its two outer edge pieces flipped relative to the center edge - just like what you'd expect from a 4x4 OLL case. Using the same OLL parity algorithm as in your 4x4 did fix it, as expected.

Since one of the final 2 edges did solve properly, I don't know what I could have done wrong.

Dominick Viel

it is not realy a parity, to solve it I do 180 turns a bit using 2 slices on the side and the top face, it flips things up then you solve the 5 edges that were undone by doing it.

Carter Eaton

If you can solve a 4x4 you only need the one algorithm listed in this guide, that's why the 3x3 and 4x4 solutions are included. I know how to solve a 4x4 and this guide was good enough.