4x4x4 Rubik's Cube - The Beginner's Solution

4x4 Cube Patterns

The Rubik's Revenge is the 4x4 version of the Rubik's Cube. This is also a Hungarian invention, designed by Sebestény Péter. This twisty puzzle can be used as a 2x2x2, not turning the outer layers or can be used as a 3x3x3 if we rotate only the outer layers. There are about 7.4×10⁴⁵ possible permutations for this puzzle.

It has 24 edges, 24 centers and 8 corner fields. It has similar core mechanism as a Rubik's Cube but in this case the 4 center pieces are held together by a hidden center. To take it apart pop out a center piece with a screwdriver.Reassembling can be hard unless you have four spare hands.

2x2, 4x4 and 5x5 cube puzzles

Variations

Just like the Rubik's Cube, the 4x4 has many shape mods, built on the same inner mechanism.

Axis Cube – cube in solved position but it changes its shape as you scramble it.
Octahedron – the centers become corners and the corners become centers.
Fisher Cube – the mother of shape mods.
Bandaged Cube – with some pieces attached together.2x2 in a 2x2 by Meffert's.
Windmill – with a slightly twisted core.
Mastermorphix – 4 colored pillowed shape shifter.
4 colored shape-shifter. We have to mention the 4x4 Ghost and Mirror cubes too.

How to solve a 4x4

The solution is more complicated than the classic Rubik's Cube method, but if you know how to solve a 3x3x3 then you shouldn't have difficulties with this one either. We solve the 4x4 grouping the 4 centers and the edge-pairs together, and finally solving it like a 3x3. Some speedcubers can solve this cube under 30 seconds so it can't be that hard!

Notation

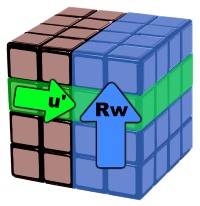We use letters to mark the rotations on the cube, similar to the the Rubik's Cube notation. Deep turns come in when we move two letters together, but we can define slice turns when we move the second layer only. We are going to use the official NxNxN notation:

F – Outer front face clockwise
U' – Outer up face anticlockwise
L2 – Double turn of the left face (180^o)
Fw – Outer block move: the two front faces together clockwise. For NxNxN cubes we mark how many layers to grab but we can ignore this for a 4x4 cube since the numbers is always 2: 2Rw'. Other tutorials use lowercase letters to mark double turns.
f – Lowercase letters mark inner slice turns. u' = Uw' U

Step 1: Two adjacent centers

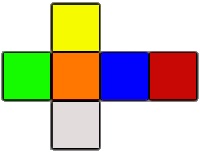Since the 4x4 has no fixed center piece which determines the color of each face we have to calculate the color scheme from the colors of the corner pieces.

The image shows the most common color scheme, which is copyrighted by the Rubik's brand so other manufacturers avoid it by replacing the orange with purple or reorganizing the faces. If you have a Rubik's logo on your cube then this is the one you have to use.

Let's solve the white and yellow adjacent centers first. If you can't find any corners having these two colors next to each other then these should be fine.

This step shouldn't be a problem because there are no solved pieces that we can mess up. Use this short algorithm to insert a piece from the top to the front layer.

Dw' Rw' Dw

When the white face is complete, Try to build the yellow 2x2 block on the opposite side with the white face moved to the bottom. 

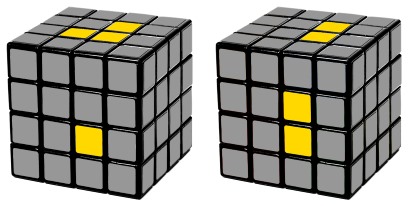
With the completed white center at the bottom: Rw U Rw' and Rw U2 Rw'

 Step 2: Remaining four centers

Move the completed centers to the left and right sides to keep them out of the way. Build the first block then keep an eye on the color scheme for the next ones.

Use the same algorithms as above, with the white and yellow centers on the left and right: Rw U Rw'

Step 3: Pairing the edges

The center blocks are done and now we have to pair the edges. Use the algorithms below to attach two edges from the front-left and front-right edges. Depending on their position we have to use two mirrored algorithms. Make sure there's no complete edge above the lower edge piece (marked with arrows) because this algorithm would break that.

When the matching pieces are side by side on the same level (3rd picture) you need to turn the one on the right upside down to be able to perform one of the moves.

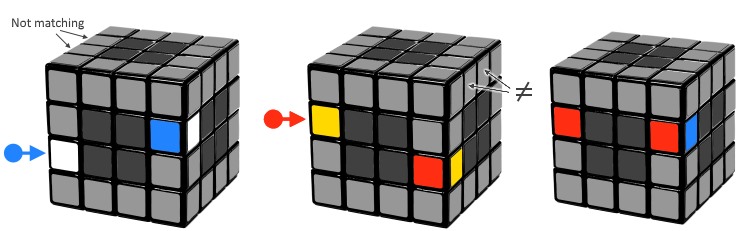
First case: Uw L' U' L Uw'     Second case: Uw' R U R' Uw     Side by side: R U' B' R2

When you reach the last two edges then you won't be able to use any non-matching edge pairs in the top layer because they all have been paird already. We have a separate algorithm to solve the last two edges. Use the R U' B' R2 trick above if the pieces are not aligned correctly.

Last edges: Dw R F' U R' F Dw'

Step 4: Solve it like a 3x3

From this point we can finish the cube solving it like a 3x3, turning the outer layers only. Read here how to solve the Rubik's Cube if you need further help but don't close this page yet because you might be facing one of the parity cases as you go further.

The 4x4 reduced to a 3x3

Step 5: Parity cases

As you reach the last layer you might find yourself in a situation where the cube seems to be unsolvable. For example when you reach the yellow cross and one edge seems to be oriented wrong or you find two pieces on the correct spot when you are positioning the last layer corners. See which of the long algorithms below solves your situation. 

Reorient 2 and 3:
r2 B2 U2 l – U2 r' U2 r – U2 F2 r F2 – l' B2 r2

The same without slice moves:
Rw2 R2 B2 U2 – Lw L' U2 Rw' – R U2 Rw R' – U2 F2 Rw R' – F2 Lw' L – B2 Rw2 R2

Swap 4 and 5:
Rw2 f2 U2 Fw2 – D Rw2 U2 Fw2 – U’ Fw2 L2 U2 – B2 Lw2 U
The same algorithm without slice moves:
Rw2 Fw2 F2 U2 Fw2 – D Rw2 U2 Fw2 – U’ Fw2 L2 U2 – B2 Lw2 U

Swap 1 and 4:
F2 R2 B' - D' B R2 F' U  - Fw2 F L2 - f2 Lw2 - f2 l2 U' (ok)
The same algorithm without slice moves:
F2 R2 B' - D' B R2 F' U - Fw2 F L2 - Fw2 F2 Lw2 - Fw2 F2 Lw2 L2 U'

More about the 4x4 Parity

Solve any NxNxN cube