The Megaminx - Easy Solution

The Megaminx, previously called as Hungarian Supernova was patented by Uwe Mèffert. It is a dodecahedron-shaped face-turning twisty puzzle which is very similar to the classic Rubik’s Cube. The solution is almost the same, just a few new algorithms come in when you reach the last layer, so if you’re familiar with the classic 3x3x3 Cube then you won't have problems solving the Megaminx either.

There are many variations but the most common version has 12 different colors, having 11 pieces in a star-pattern arrangement on each face with five corner pieces, five edge pieces and a fixed center piece. It has a total of 50 separate pieces.

Start the Megaminx simulator

The Megaminx is an official WCA competition event. The World Record is held by Leandro Martín López (Argentina) with 23.18 seconds. result.

On the image above a white and a black-body Megaminx is accompanied by their smaller brother, the 2x2 Kilominx (Flowerminx), a dodecahedron-shaped Rubik's Cube shape mod and a 3x3 cube. The bigger dodecahedrons are called Gigaminx, Teraminx, Petaminx, Zettaminx, all the way up to the record-breaking Yottaminx (image below).

Solution of the Megaminx

To solve the Megaminx first you need to know how to solve the Rubik's Cube because the methods of the two puzzles are very similar. There are a few steps where you might get stuck but the algorithms below will help you go through the difficulties. 

Let's use the same FRU notation that you are probably familiar with. Each letter means a clockwise rotation of the face, while apostrophes mark the anticlockwise turns. Note that in this case F2 = F'3 and F'2 ≠ F2.

1. White face

The start is similar to solving the white cross on a Rubik's Cube. Fill the gaps between the white and side centers with the matching colors. In this case we're not building a white cross, but a white star on the top.

When the edges are done insert the white corner pieces, just like you would for a Rubik's Cube.

This step is really intuitive and it shouldn't be a problem, try to do it without checking the links.

2. Second layer

Turn the cube with the solved face down and use the same F2L algorithms that you already know from the 3x3 to solve the next set of edges. When they're are all done, locate the corners above each completed edge and turn them where they belong to.

3. Third layer edges and corners

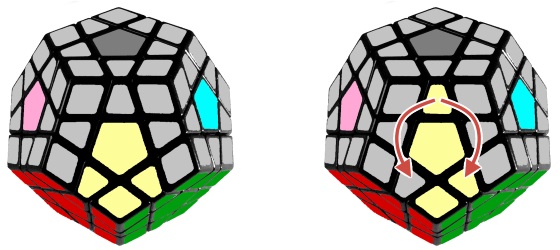
This is the first step where you might need a little help, even if you know the 3x3 solution. Use the left or right algorightms below to insert the marked pieces from the top layer:

Left:  F' R' F'2 R F
Right: F L F2 L' F'

When the edges are in place go ahead and solve the corners. Use the same method that you used for solving the white corners.

4. One more time

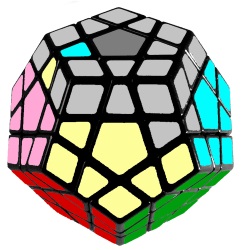
We've reached a point where we have to perform another set of "first layer corners" and "second layers", but we already know how to do these.

5. Top star

For the Rubik's Cube we call this step solving the yellow cross. We can use the exact same algorithms but here we have to form a star, not a cross on the top of the puzzle.

First case (flips F and R edges): F U R U' R' F'
Second case (flips F and B edges): F R U R' U' F'

6. Cycle edges

This step is similar to swapping the yellow edges on the Rubik's Cube. The algorithm is the same with a small tweak: instead of making U2 we have to make U3 in the clockwise algorithm. 

We can cycle three edges on the front face of the Megaminx in the desired direction with the algorithms below. The two algorithms are the inverse of each other.

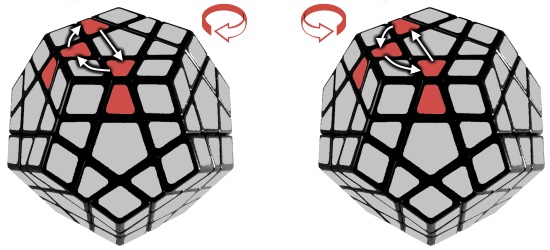
Clockwise: R U R' U R U3 R' U
AntiClockwise: U' R U2 R' U' R U' R'

7. Cycle corners

Positioning the last layer corners is the penultimate step before completing the puzzle. There are two algorithms that cycle the corners as shown on the image below.

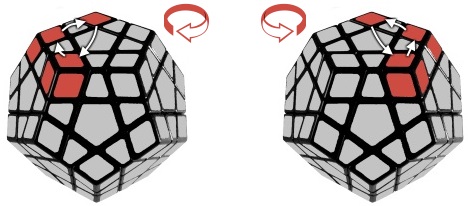
Clockwise: L' U2 R U'2 - L U2 R' U'2
Anticlockwise: R U'2 L' U2 - R' U'2 L U2

8. Orient corners

However the algorithm is simple, orienting the last layer corners is the most confusing part of the Beginner's Method. 

Doing U rotations bring the unsolved corners to the highlighted position one by one. Repeat the R' D' R D algorithm for each piece until they are all positioned correctly.

R' D' R D

Online Megaminx Simulator