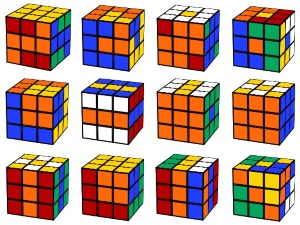
4x4 Rubik's Cube Patterns and Algorithms
Ever since the dawn of cubing, we have liked patterns for a number of reasons, including their predictability, their aesthetically pleasing features, and their adaptability.
How to make your own patterns
Patterns are pretty much limitless, even more so on 4x4 than on 3x3, mostly due to parities and slice moves. As they are a kind of art form, one cuber can think it looks bad, while one can think it is beautiful. To make your own, what I usually do is just play around with the cube. However, you can also start with an existing pattern and then make some changes to it, do algorithms that mirror switches like M2 U2 M2 U2.
Most patterns tend to mirror each other, so OLL parity won't play a huge role in the creation of patterns, but PLL parity is worth a mention. The fact that the 4x4 has these parities makes it easier to make patterns, as you have more freedom. Some designs will use parities to mirror on only one axis or layer.
Of course, you will also want to undo the patterns. To do this, you can either just solve the cube normally, or you can undo the algorithm. The latter is recommended as it tends to be quicker than solving the cube normally, especially for shorter algorithms such as the simple checkerboard [image]:
M2 E2 S2.
Making cube patterns with the Cube Solver
Generate and visualize 29 patterns with the online Rubik's Cube solver. These designs work on any NxNxN Puzzle Cube not just on the 4x4. Open Cube-Solver.com, and pick the size of the cube to get started then select the "Patterns" menu item. You'll see the names listed:
Anaconda, Cross, Cube x2, Cube x4, Cube x4 Twisted, Checkerboard, Checkerboard1, Checkerboard In Cube, Corner Pyramid, Displaced Motif, Exchanged Duck Feet, Four Crosses, Gift Box, Perpendicular Lines, Pyraminx, Python, Six Spots, Six Spots + Cross, Six-Two-One, Spiral, Staircase, Twin Peaks, Twister, Union Jack, Vertical Stripes, Viaduct, Weirdo, Wrapped 2x2, Yin Yang
Select a name to display the scramble algorithm. You can click through the steps as you follow the turns.
Reversing an algorithm
Sometimes it can be quite hard to undo a pattern, as all the moves need to be reversed.
For example, the algorithm
F L F U' R U F2 L2 U' L' B D' B' L2 U
would need to be reversed to
U' L2 B D B' L U L2 F2 U' R' U F' L' F'
As you can see, the algorithm itself is reversed, i.e. you start from the end, and the moves are reversed; U becomes U', U' becomes U, and technically U2 becomes U2', but since they affect the cube in the same way, they are not necessary to reverse. Slice moves such as r2 or r' stay on the right side, they are just reversed the same as outer layer turns.
How to read the notation
4x4 notation is based on 3x3 notation. The normal 3x3 moves U D R L F B M S E
are the same outer layer turn on the 4x4.
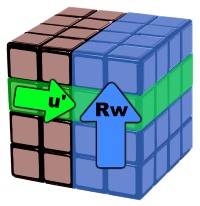A lowercase letter such as r or u means that you move the inner layer of that side.
For example a r’ move means that you move the inner right layer in the same direction as R’, so down.
M, S, and E moves are never written as lowercase, as there are no sides or slices that they could refer to, at least not on 4x4.
There is one more type of move that is used on the 4x4, and that is the wide moves or double layer moves. These moves are Uw, Dw, Rw, Lw, Fw, and Bw.
These moves go in the same direction as the non-wide moves: Rw goes in the same direction as R and Rw’ goes in the same direction as R’. They are the outer layer and the slice layer on that side.
Read more abour the advanced notation here.
Examples
Small box big box
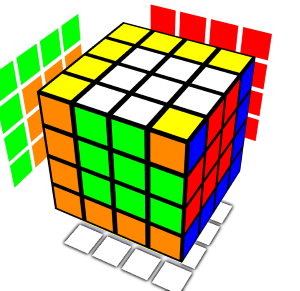
B' U' B' L' D B U D2 B U L D' L' U' L2 D
Corner wrapper
L U B' U' R L' B R' F B' D R D' F'
3x3 in 4x4
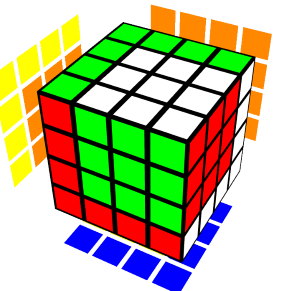
F L F U' R U F2 L2 U' L' B D' B' L2 U
Opposite boxes
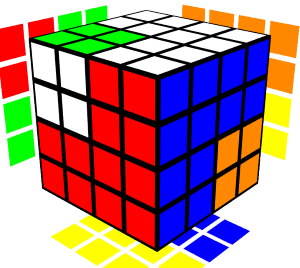
Bw2 Rw' Dw Rw Dw' Rw' Dw Rw Uw
Rw' Dw' Rw Dw Rw' Dw' Rw Uw' Bw2
Rings
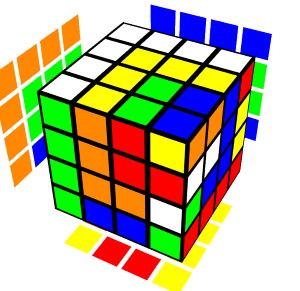
B' M2 U2 M2 B F2 R U' R U R2 U
R2 F' U F' Uw Lw Uw' Fw2
Dw Rw' Uw Fw Dw2 Rw2
