God’s Number
Mathematicians love the Rubik’s Cube. There’s no denying it. They are amazed at how such a seemingly simply puzzle can hold so many secrets. There is always something new to learn about the cube (if you are willing to learn, of course). Perhaps the biggest secret of all, one that took over 30 years for mathematicians to crack is God’s Number.
God’s Number, as many cube enthusiasts will already know, is the maximum number of moves required to solve any of the 43,252,003,274,489,856,000 combinations of the cube. It has been proven that this number is 20 (cube20.org), however the discovery is fairly recent (July 2010). The term “God’s Number” was coined because the mind of a being able to find the shortest sequence of moves to solve any scramble sequence would have to be thousands of times more powerful than our own, able to test millions of different combinations in the blink of an eye, something that mathematicians believe only a Deity could possess.
This number may seem low, but theoretically it should be even lower. Only around 490,000,000 combinations require the full 20 moves to be solved. Although 490 million is a huge number, it is only a fraction of the 43 quintillion possible combinations (0.0000011328955% to be precise). The chances of generating a random scramble that can only be solved in 20 moves, no more no less, is around 1 in a billion. However, the number of combinations that can be solved in 19 moves is approximately 1.5 quintillion. This means that God’s Number is much closer to 19 than 20, but unfortunately even if only 1 scramble sequence was impossible to solve in less than 20 moves, God’s Number would still be 20.
The Super-Flip
Perhaps the most famous of the rare scrambles that require exactly 20 moves to solve is the super-flip position (pictured). This is achieved by performing the following sequence of moves - R L U2 F U’ D F2 R2 B2 L U2 F’ B’ U R2 D F2 U R2 U from any orientation. The position is recognisable as every single corner is solved in its place, while every single edge is flipped in its place. This was also the first position that was found that could not be solve in less than 20 moves, raising the lower bound of God’s Number to 20 in 1995.
History of God's Number
Work began on the search for God’s Number back in 1981, when a man named Morwen Thistlewaite proved using a complex algorithm he devised himself that 52 moves was enough to solve any of the 43 quintillion different scrambles. This number began to fall slowly as better, more efficient methods were devised for solving the huge number of possible combinations in the fewest moves possible.
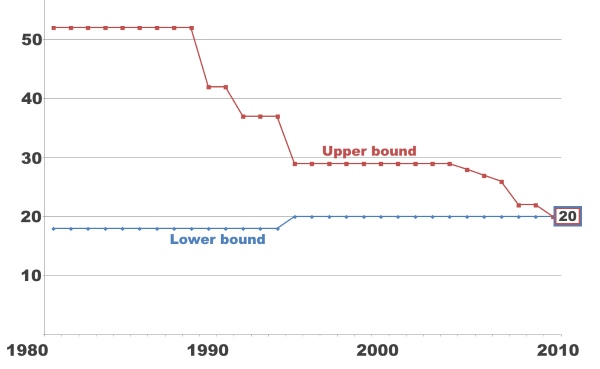
Of course, not all 43 quintillion combinations were tested individually by computers. Many ingenious patterns were spotted to reduce this number to a fraction of its original quantity. For example, if you were to perform the super-flip algorithm on a Rubik’s Cube and rotate the entire cube by 180 degrees, you would have theoretically created another of the 43 quintillion combinations without increasing the number of moves required to solve it. The reason for this is because 43 quintillion is the number of positions, not the number of completely unique patterns. If you were to hold the white face on the top and the green face on the front, that would be one position. If you were to rotate the puzzle so you are still holding the white face on the top but instead you had the red face on the front, you would have another position. Therefore, by multiplying the number of different possible “top faces” (6, one for each colour) by the number of different possible “front faces” for each different “top face” (4), you would be left with 24 different ways to position the cube for any given state. This automatically reduces the enormous number of 43 quintillion possible positions that would actually need to be tested to 1,802,166,800,000,000,000 (a mere 4% of the original number). By factoring in other similarities such as mirrors, this number reduces further, making God’s Number much easier to calculate.
Two different “positions” out of the 43 quintillion possible
God’s Number can also be implemented for other twisty puzzles, such as using an original Rubik’s Cube with certain restraints, or using smaller or bigger puzzles. God’s Number for a Rubik’s Cube solved using only quarter turns (where no face can be rotated more than 90 degrees at a time either clockwise or anticlockwise) has been proven much more recently (2014) to be 26 moves.
God's Algorithm for 2x2x2 Cubes
God’s Number for the 2x2 puzzle (having only 3,674,160 different positions) has been proven to be 11 moves using the half turn metric, or 14 using the quarter turn metric (half turns count as 2 rotations). Unfortunately God’s Number has yet to be calculated for the 4x4 cube, or higher.
The Devil's Number
As we have discussed on the Mathematics of the Rubik's Cube page, every algorithm (permutation) has a degree in group theory. Every sequence of moves, if repeated enough times, will return the cube to the original state. For example a simple face turn needs 4 repetitions, the R' D' R D algorithm needs to be applied six times, going through 24 states.
Obviously, there's an algorithm that goes through all 43,252,003,274,489,856,000 possible positions of the cube. If we would apply this algorithm to any random scramble then it would certainly go thorugh the solved state at some point.
The Devil's algorithm is about about looking for the smallest number of moves needed to visit every position at least once. One algorithm, that applied repeatedly to any scramble will return to the solved state, not necessarily at the end of of the sequence. Devil's Number is the amount of moves in the shortest algorithm that does this.
Imagine that you could solve the Rubik's Cube knowing just one algorithm. The problem is that this would be extremely long. Finding the Devil's algorithm is much much harder than finding the optimal solution.
The fact is that we still don't know the Devil's algorithm for the 2x2x2 cube, despite that it has much fewer possible positions. So don't expect this to be found for the Rubik's Cube any time soon. Unfortunately the numbers are so imaginably high that even the 2x2x2 attempts have failed.
Let's see an example for the Devil's algorithm. If we scramble a 2x2x2 cube allowing only half turns, we can come back to the solved position repeating the following: R2 U2 R2 U2 R2 B2 R2.
Fewest move challenge in official competitions
In official Rubik’s Cube competitions organised by the World Cube Association (WCA), there is an event called Fewest Move Count (FMC), which involves taking a random computer generated scramble and solving it in as few moves as possible. A computer would be able to find the most efficient solution possible that takes the least amount of moves in seconds, however in this event competitors have 1 hour to try and find the most efficient solution that they physically can. The World Record for this event went below 20 moves many times. In 2019 Sebastiano Tronto (Italy) found a solution on an official competition in 16 moves. Keep track of the evolution of FMC records on the official WCA website here.
To conclude, God’s Number is a fascinating theory. It shows us how such a simple looking puzzle can have over 5 and a half times more combinations than there are grains of sand on the Earth, and it also proves that computers will always be infinitely better than humans at almost any task.
Computer programs
The Cube Explorer program by the German mathematician, Herbert Kociemba is able to find the optimal solution in 20 steps using the half turn metric (half turns count as one move). Test our program which is using the same algorithm. It's looking for the solution in 20 moves but if the program doesn't return any result below the time threshold then it switches to 24 steps which is also very close to the God's number.
Close-to Optimal Rubik’s Cube Solver »
M = L' R X''
Your formulation of the Devil's algorithm: "an algorithm which needs the biggest number of repetitions to return to the starting position" is wrong. The number of repetitions needed to arrive at the starting point is called the order (Ord) of an algorithm. It is maximally 1260. You give a correct example of this by considering that Ord(R' D' R D) = 6.
--
The Devil's algorithm is an algorithm that "when applied, repeatedly if necessary, will eventually return a Rubik's Cube to a solved state regardless of the starting configuration." (See http://anttila.ca/michael/devilsalgorithm/).
--
But even here, the phrase "will return the Cube to a solved state" is ambiguous. Do we mean the end result of the alg, or all the intermediate states? That needs to be part of a correct definition. Now will follow a definition that I think is precise enough for our purposes. Of course, it will coincide what everybody thinks it means. The power lies in its formulation to be unambiguous (I hope, fingers crossed.)
--
What we really want is to define the set of all the states an algorithm goes through during its application. Obviously, if its length is N, the number of states will be no greater than N.
Definition. For any alg X, let X_1 := X and X_(n+1) := (X_n X) for n > 0 an integer.
Note. X_n denotes X repeated n times. We also normally denote X1, X2, X3, etc. without the underscore. It is used here to avoid confusion, as I was using an index of (n+1).
Definition. For any alg X starting with turn T, let X = (T R[X, T]) where R[X, T] denotes the rest of the algorithm X following T. Let X(1) := T and X(n+1) := X(n) R[X, X(n)](1) for n>0.
Note. X(n) denotes the first n moves of alg X.
Definition. Let Reach(X) be the set of states that are the end result of the algs X(1), . . . , X(n), each applied to a clean cube. We say that X reaches the states Reach(X).
Definition. For any set S of algs, Reach(S) is the union of the Reach(X) over all X in S. We say that S reaches the states Reach(S).
Definition. A Devil's algorithm is an algorithm X, such that the set of algs X_n (n>0) reaches ALL 43 quintillion possible states of the cube.
Pfew. Getting some water.
Note. There may be more than one Devil's algorithm. In fact, it is more than likely! Whether the criterion should be "shortest" or "reaches all states exactly once" is debatable. Perhaps the algorithm that is the shortest reaches some (but not necessarily all) states more than once. We wouldn't dismiss it for that reason, would we?
The power of the Devil's algorithm is that it will eventually reach the state which corresponds to the "solution" of any given (reachable) state of the cube. Since we know the maximal order of an alg is 1260, we know that the Devil's algorithm needs to have at least 43 quintillion / 1260 = 34,326,986,725,785,601 turns.
--
I hope this helps to clarify this subject a bit.
Hello, I'm Brazilian and my English may be a bit bad, but it's the following:
There is an App (rubiks-cube-solver.com) that says solve the magic cube in 20 moves or less as was said on this page.
But I found a scramble that he solver can only solve in 22 moves!
The sequence is this:
B2 D2 F2 R2 D L2 U2 B2 F 'L D B' F' U2 L U R2 D' B' R2 F' R'
This was the fastest solution (which needed fewer moves) that the app was able to generate.
This shuffle is the set of Super-flip that reverses all means,
With another shuffle (I do not know the name) that inverts all the corners, leaving all the pieces of the cube inverted but in their proper places.
1. a graph representing the faces and the effect of any permissible operation, s.t. an initial cube state assigns an initial value to any node. Then, any algorithm is a set of operations.
2. a graph wherein each node is a state of the system (cube). There are 43 quintillion nodes. Each node connects to 14 other nodes. Therefore, any solution from any node is any path through this graph which leads to the one, chosen state.
The God's Number claims there are only 20 steps from any node to any other node in graph 2.
The Devil's Number is the Traveling Salesman Problem, to visit every node in the least steps.
There should be (might be?) a least algorithm which permits moving from any 20 steps distant state to any other in graph 2.
So, Graph 1 are the rules which allow you to move from any state to another state in Graph 2. Of course, the graph 1 encodes the 14 possible transformations, but each edge in graph 2 is just one of the graph 1 transformations.
You could mess around with graph 1, removing or adding any edge between two nodes, or removing/adding nodes. This, of course, usually does not map to any central-vertex rotational puzzle that can be constructed in 3D space-time. You can make n^2-tile cubes, and k-dimenzional. Each being a graph 1. Any graph 1 generates a graph 2. But few Graph 2 state spaces can be defined by a simple graph 1. Mazes come to mind. Infinite mazes - even worse. Infinite mazes made of infinite connections to other infinite mazes at every vertex, are all the rage nowadays. Tessellations have a graph 1.
This formulation, I think, can be applied to any discrete system where there exists a graph 1 encoding the rules (physics) of the system. Thus, Physics itself, attempts to find the minimal definition of reality as the quantum or string states that can be encoded as states in graph 2, and the rules/laws of physics encoded in graph 1. I think the calabi-yau 11 dimensional shapes of super-string theory are put to this formulation, and it has been found that a minimal graph 1 exists that represents our reality. There are, due to the 'Constants of Nature' many many permutations of the graph 1 which are not our reality, many of which generate graphs 2, that themselves have embedded intelligent entities contemplating the graph representation of their reality, all realities, and the computational complexity of finding a path from any node to any other node.
Well, that was fun. Thoughts and ridicule welcome!